●再度、問題文を読み返し、誤認・誤記等の有無を確認

　し、正しいとの判断の下、求めた相互の具体的数量を

　用いて問題文通りの割合値になっているか等の見直し

　をする。


●更に、問題文を読み返し、答えにあたるものが何かを

　確認し、立式等を通じて求める。


●最後に、見直し…。

●一般的には、はじめの全体の数量を示すのに用いた

　種類の比にそろえ、線分図中に記入する。

　ここでは、

　□比のすべてを「仕入れ値」＝①の○比にそろえる。

探すことができましたら…

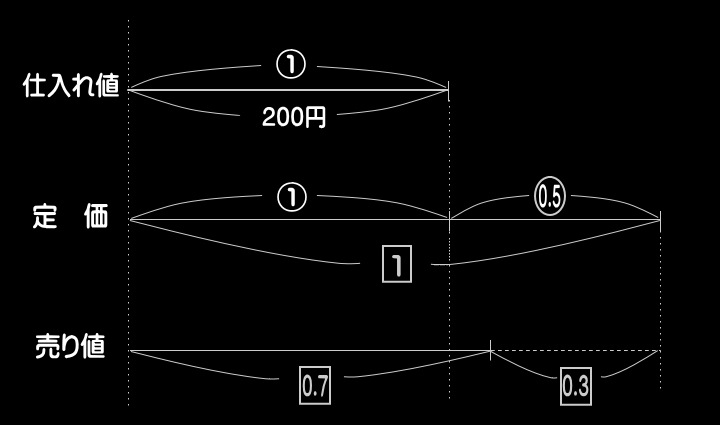
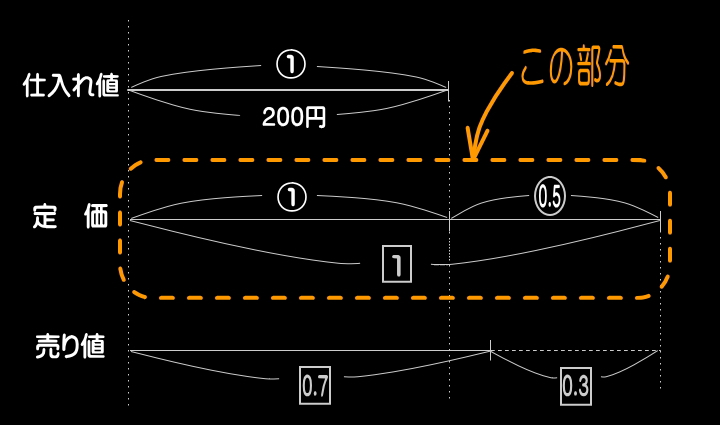
●売り値について、

　「定価の３０％引き」なので、基準となる全体量は

　　①（仕入れ値）ではなく、定価となる。

　よって、異なる種類の比（□）を用いて示す。

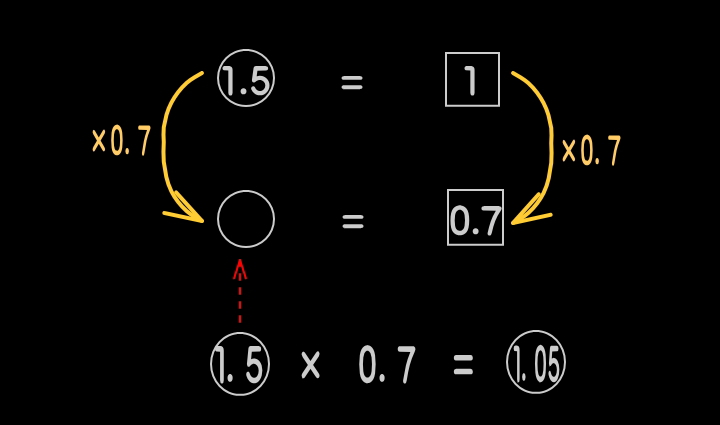
丸覚えした下記の式を用いて、進める。

下記の手順をふみながら、解き進める。


●仕入れ値、定価、売り値のそれぞれについて、
　比、具体的数値などを記しながら、線分図を作成する。


●比をそろえる作業をする。


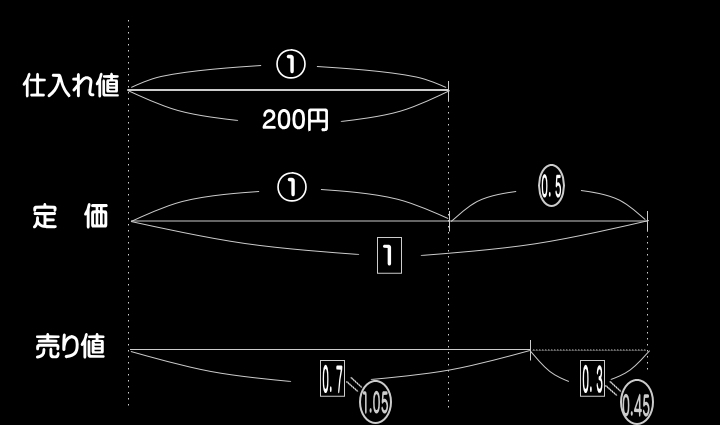
●「①」（＝仕入れ値）の具体的数量を求め、線分図中に

　示す。


●再度、問題文を読み返し、誤認・誤記等の有無を確認し
　
　、正しいとの判断の下、求めた具体的数量を用いて、

　見直しをする。


●最後に、答えにあたるものが何かを確認し、
　
　立式等を通じて求める。

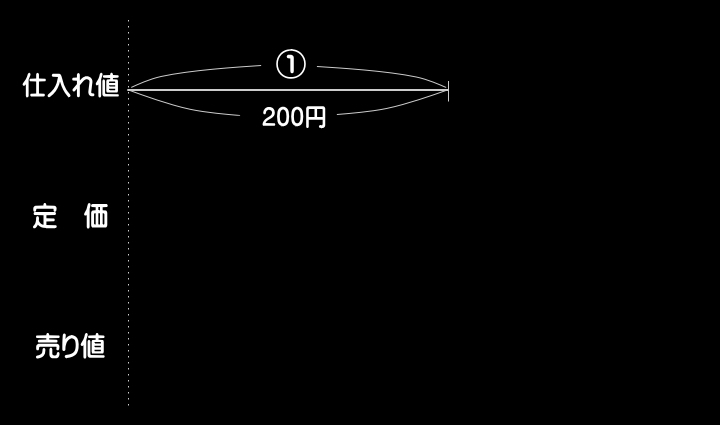
●仕入れ値＝①とおき、次の手順をふみながら、

　下図のような線分図を作成する。

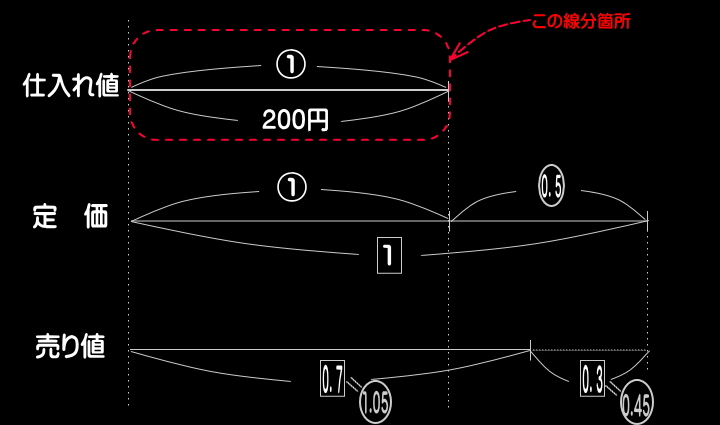
●探した比と具体的数値との関係を式に示す。


　⇒ただし、この例では、解き始めに「①＝２００円」と

　　定めているので、この作業は必須ではありません。

●更に、上図を見て、比と具体的数量の双方で示されて

　いる線分箇所を探す。

●比をそろえる作業に移る。

　上図を見て、異なる2種類の比の双方で示されてい

　る線分箇所を探す。

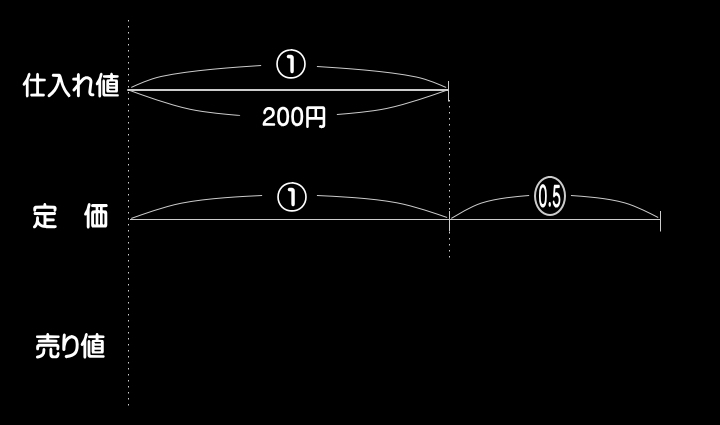
●定価について、

　基準となる全体量は①（仕入れ値）であるので、

　同じ種類の比（○）を用いて示す。