Ｎ（正の整数）の約数を求める場合、

　「 １ ～ Ｎ 」までの整数のうち、小さい整数から順に

　暗算でＮの除法を行い、割り切れるとき、

　下記のように、

　「わる数」を分母に、「商」を分子に書き示し、

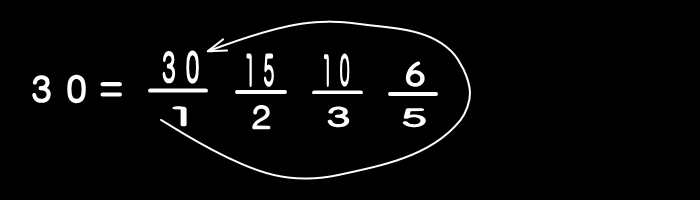
　既に分子に示されている整数でＮをわる前段階まで

　繰り返す。


　たとえば、「３０」の約数を求める場合…。

　Ｎ（正の整数）の約数を求める場合、

　「 １ ～ Ｎ 」までの整数のうち、小さい整数から順に

　暗算でＮの除法を行い、割り切れるとき、

　下記のように、「わる数」と「商」を順に書き記す。

　たとえば、「３０」の約数を求める場合…。

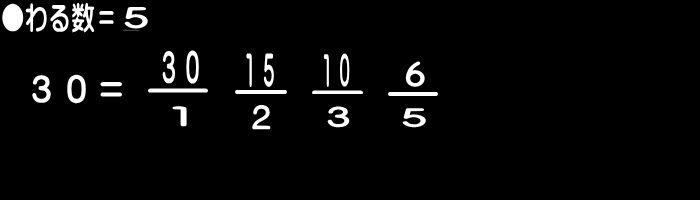
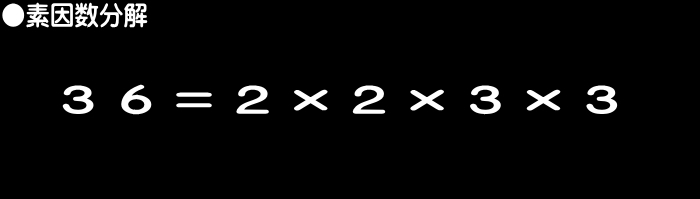
　Ｎ の約数を求める場合、
（正の整数）　
　　　「素因数分解」 ⇒ 「場合の数（組合せ）」

　の処理手順に従う。


　たとえば、「３６」の約数を求める場合…。

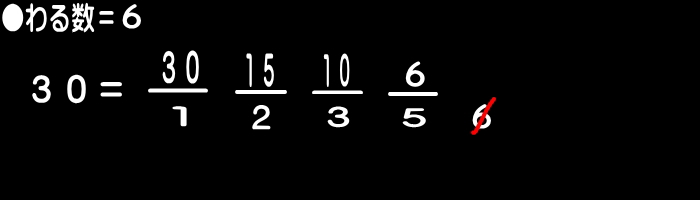
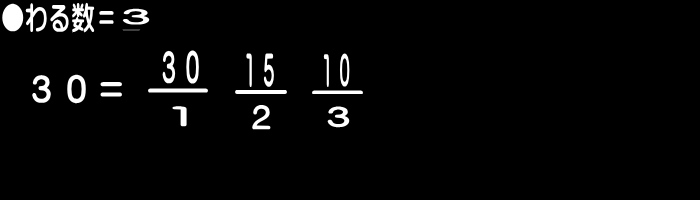
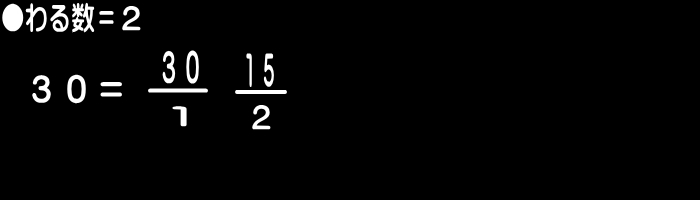
　Ｎ（正の整数）の約数を求める場合、

　「 １ ～ Ｎ 」までの整数のうち、小さい整数から順に

　暗算でＮの除法を行い、割り切れるとき、

　その整数を順に書き出していく。



　　たとえば…

　　　「 １５の約数をすべて求めなさい。　」
　
　　の問いに対して、

　　頭の中で、

　　１５ ÷ 1 ＝１５、割り切れる。＂１＂を解答欄に記入。

　　１５ ÷ 2 ＝１５、割り切れない。　　
　　
　　１５ ÷ 3 ＝１５、割り切れる。＂3＂を解答欄に記入。
　　　・
　　　・
　　　・