下記のような順に従って、解き進める。


●与えられる数列を、詳細な数式図に書き示す。


●「通し番号」と「等差の個数」との関係を読み取る。


●『○番目の数』を求める式を立てる。


●問題文を読み返し、求めるものが何かを再確認し、

　自ら立てた式を中心に、立式・計算等を通じて、

　答えを求める。

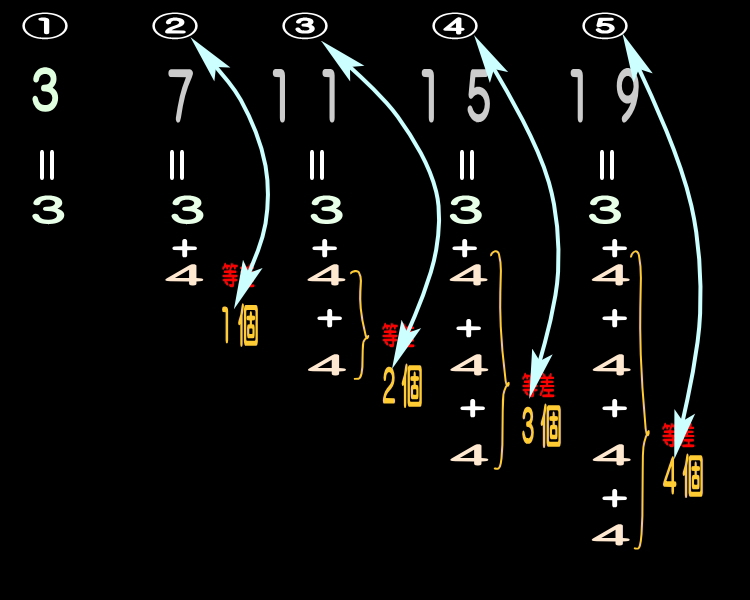
●上記の数列を数式図に示す。

丸覚えした下記の式を用いて、進める。



　　〇番目の数＝はじめの数 ＋ （ 〇ー １ ） ×＜差＞

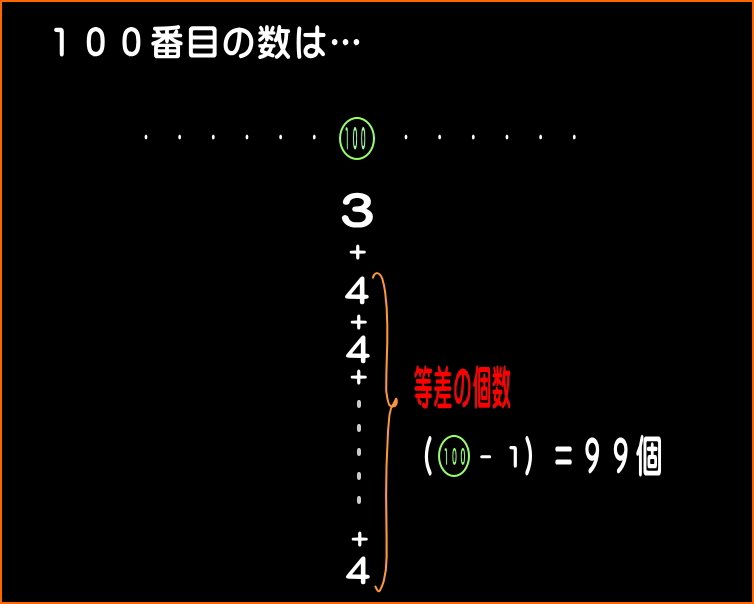
１００番目の数は、「３」に、番号の「１００」より

「１」小さい９９個の等差を加えた数だから、

「○番目の数」を求める式は、…。

●「通し番号」と「等差の個数」とを見比べる。

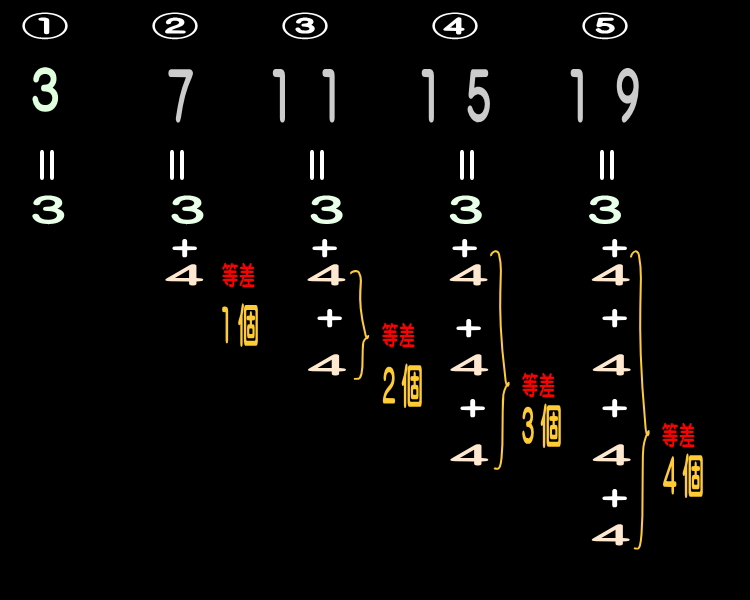
●「○番目の数」を求める式を立てる際、このまま抽象

　的に進めずに、上記の関係に対する理解のもと、
　
　たとえば、「１００番目の数」の場合…、と考え、

　下図を想像しながら、求める式を立てる。