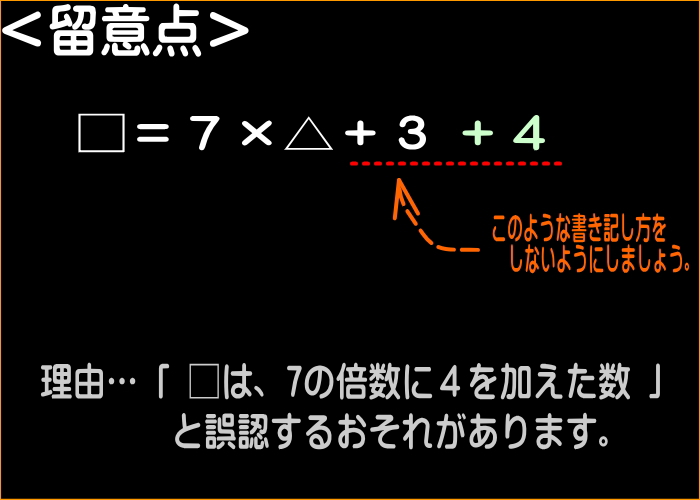
● □ = 7 × △ + 3
⇒ □は、あと「4」大きければ、7の倍数
⇒ □は、7の倍数に4足りない数
□ = 9 × ◇ + 5
⇒ □は、あと「4」大きければ、9の倍数
⇒ □は、9の倍数に4足りない数
●以上より、
□ = 7 と 9 の公倍数よりも 4 小さい数
= ( 7 と 9 の公倍数 ) ─ 4
●問題文の内容を、式に素直に書き記す。
□ ÷ 7 = △ ......3
□ ÷ 9 = ◇ ......5
●除法式を変形し、乗法式を書き記す。
□ = 7 × △ + 3
□ = 9 × ◇ + 5
●この乗法式の「(元)わる数」と「(元)余りの数」との
関係を注視し、「(元)わられる数」がどのような数で
あるかを式に書き記す。
丸覚えした下記の内容に従って、進める。
《 「余りの数」が同じ 》
⇒ 求める公倍数 + 「余りの数」
《 「不足する数」が同じ 》
⇒ 求める公倍数 - 「不足する数」
《 それ以外 》
⇒ 下記参照
下記のような順に従って、解き進める。
●問題文の内容を、式に素直に書き記す。
●除法式を変形し、乗法式を書き記す。
●この乗法式の「(元)わる数」と「(元)余りの数」との
関係を注視し、「(元)わられる数」がどのような数で
あるかを式に書き記す。
●問題文を読み返し、上式に従って、答えを求める。
| EXAMPLE |
ある数を7でわると3余り、9でわると5余る数のうち、
500に最も近い数を求めなさい。
|