次のような手順に従い、解き進める。
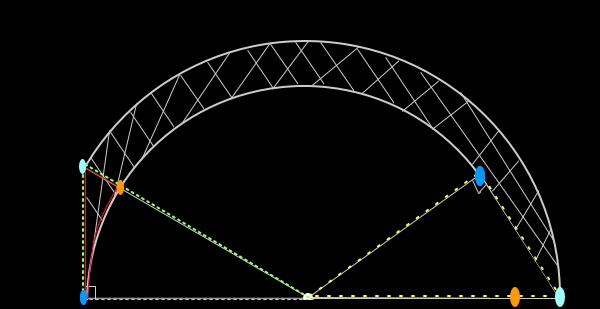
●与図をみて、
"回転前の三角形"と"回転後の三角形"
を探し、各々を太線or点線等で囲む。
●"回転前の三角形"の内部と
"回転後の三角形"の内部との双方を見比べ、
求める面積の一部が含まれている三角形を見る。
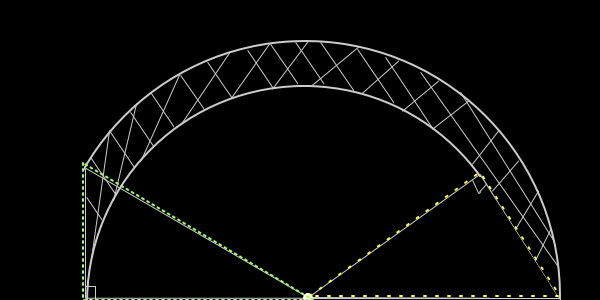
●この一部の面積だけを
◇形状をそのままに、
かつ、
◇同じ位置に、
他方の三角形の内部へ移動する。
●移動後の与図を見て、手がかり等を探す。
●問題文を読み返し、問われているものを再確認し、
立式・計算処理等を通じて、答えを求める。
●最後に、見直し…。
たとえば…。
●与図をみて、
"回転前の三角形"と"回転後の三角形"
を探し、各々を太線or点線等で囲む。
特に、基本となる手順・解き方に従わず、
与図に書き込みなどをすることもなく、
漫然と与図を眺めながら進める。
●この一部の面積だけを
◇形状をそのままに、
かつ、
◇同じ位置に、
他方の三角形の内部へ移動する。
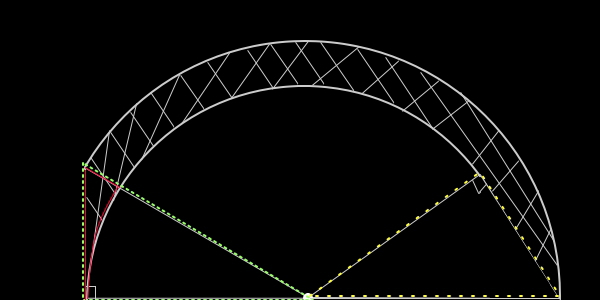
●問題文を読み返し、求めるものを再確認し、
与図に、角の大きさなどの条件を記入し、
辺の長さ等に注意しながら、立式・計算処理等を通じ
て、答えを求める。
●最後に、見直し…。
●"回転前の三角形"の内部と
"回転後の三角形"の内部との双方を見比べ、
求める面積の一部が含まれている三角形をみる。
| EXAMPLE |
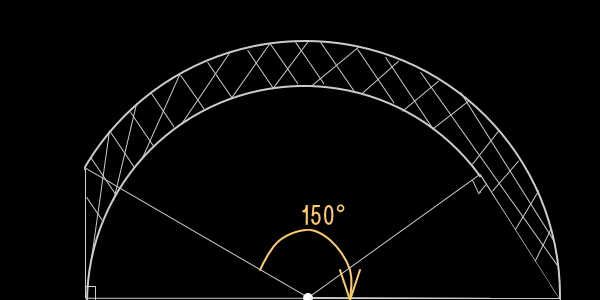
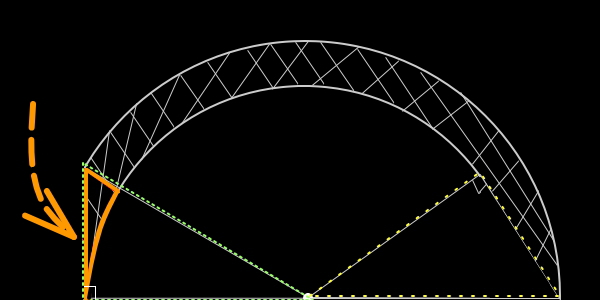
下図の斜辺の長さが10cmの直角三角形を、ひとつの頂点を中心点として、150°回転させます。このとき、斜線部分の面積は、何c㎡ですか?
|