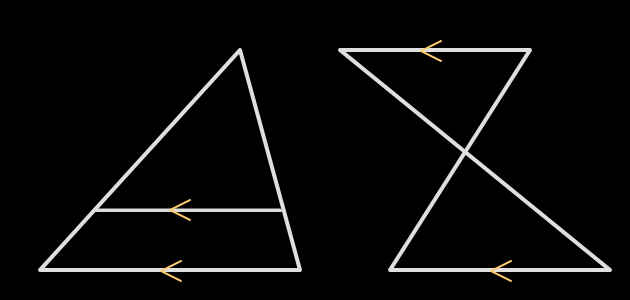●上記の"相似比"を用いて、求める辺の長さ等を、
立式・計算処理等を通じて、求める。
★求めた"辺の長さ"等の具体的な数値は、
必ず、与図に記入する。
たとえば、…。
次のような手順に従い、解き進める。
●問題文を読み、その中に含まれている条件を、
与図にくまなく記入する。
●与図中に"平行線"が含まれているか、を見る。
↓含まれていれば…。
(ただし、例外あり。)
●上記の平行線上にその1辺が重なっている三角形
のうちから、2つの相似な三角形を探す。
その際、下図("ピラミッド"or"砂時計")を
念頭におきながら、探す。
特に、基本となる解法には従わず、
与図を見て、自身が必要だと判断した箇所にのみ、
"比"や"辺の長さ"等を記入し、立式等を行い、
進める。
●問題文を読み返し、上記の"相似比"を用いて、
辺の長さやその比等を、立式・計算処理等を通じて
、求める。
●最後に、見直し…。
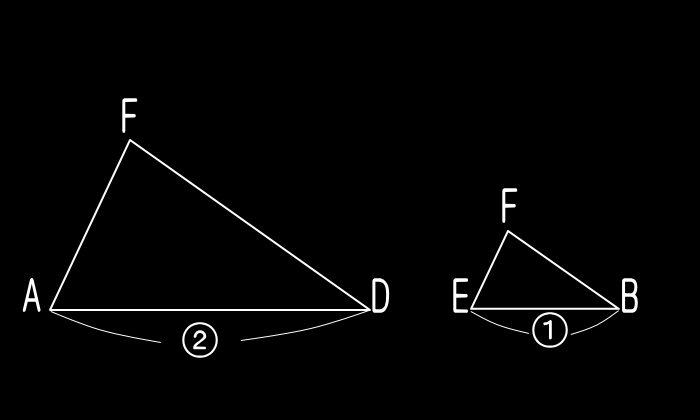
●2つの相似な三角形について、その"相似比"を
対応する各辺に、くまなく記入する。
与図を白紙に近い状態にしたままで、
立式等を行い、進める。
探すことができましたら…。
●上記の平行線上に、その1辺が重なっている三角形
のうちから、2つの相似な三角形を探す。
●2つの相似な三角形について、与図に書き記した
条件等に基づいて、その"相似比"を求める。
●与図中に"平行線"が含まれているか、を見る。
●2つの相似な三角形について、与図に書き記した
条件等に基づいて、その"相似比"を求める。。
●2つの相似な三角形について、その"相似比"を
対応する各辺に、くまなく記入する。
●問題文を読み、その中に含まれている条件を、
与図に、くまなく記入する。
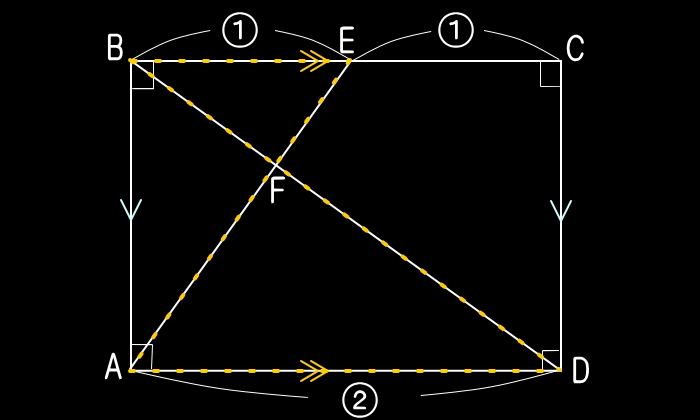
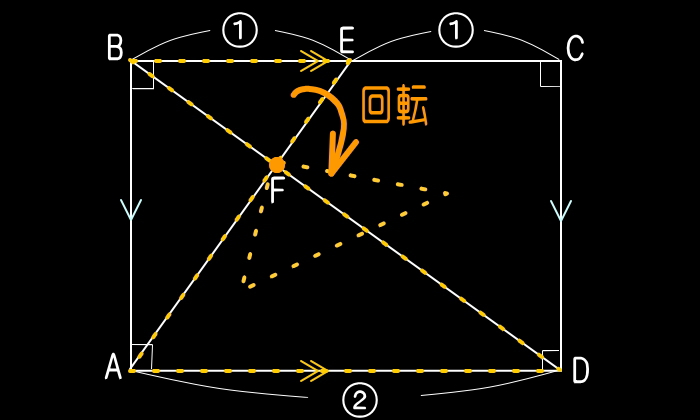
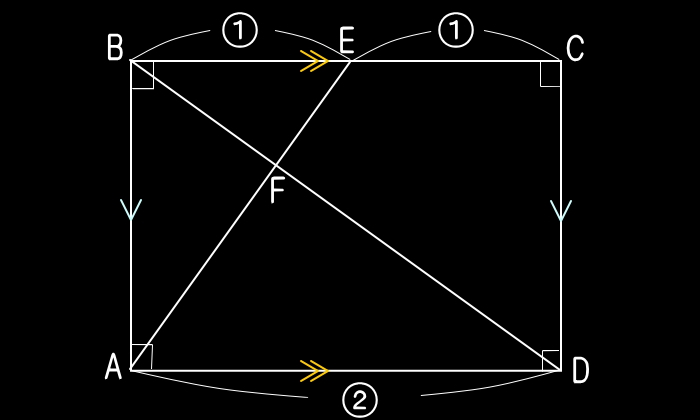
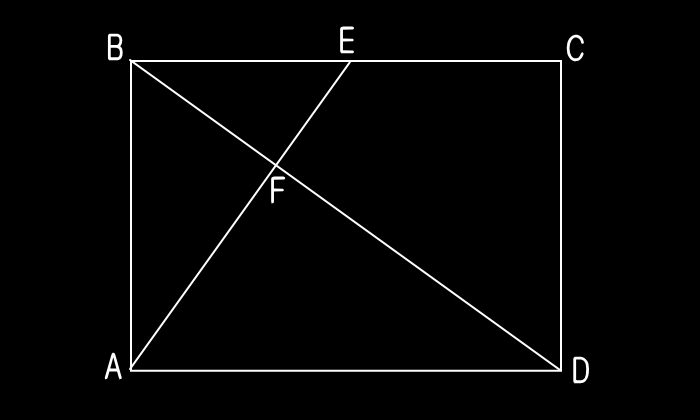
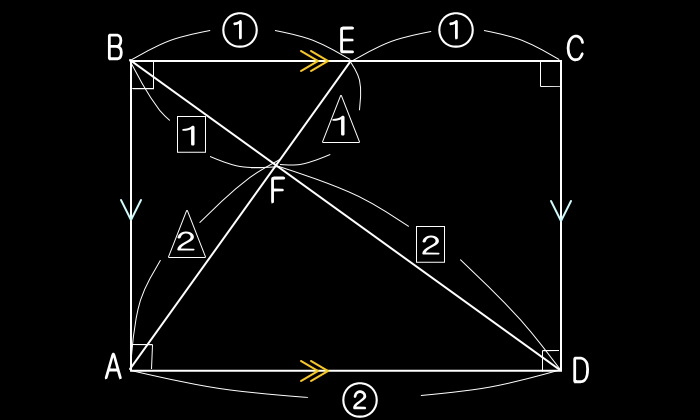
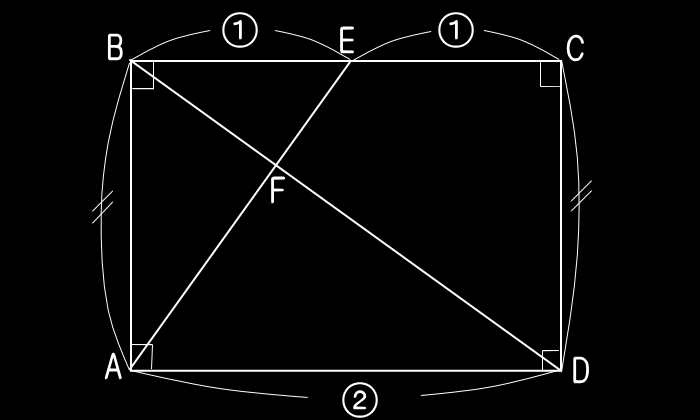
| EXAMPLE |
| 長方形ABCDがあります。辺BCの真ん中にE点をとり、これとA点を結んでできる線分と、B点とD点とを結んでできる線分との交点をFとします。このとき、辺AFと辺FEの長さの比(AF:FE)を求めなさい。 |