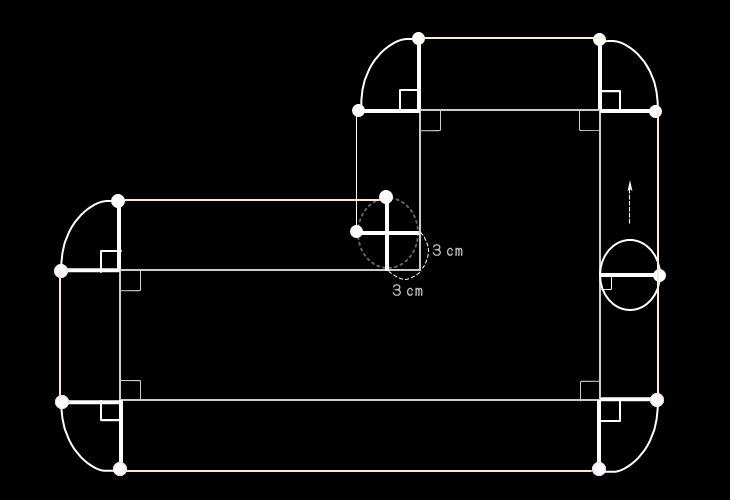
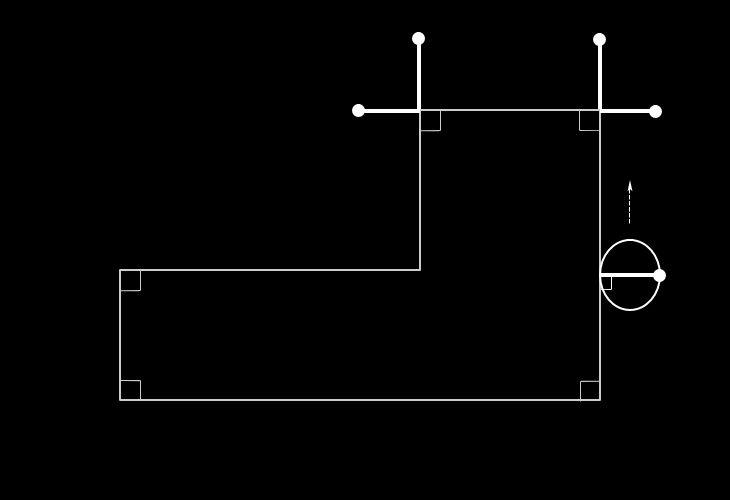
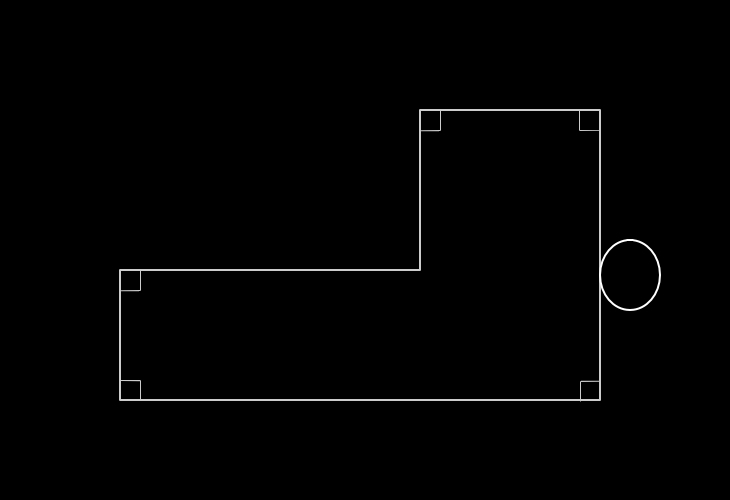
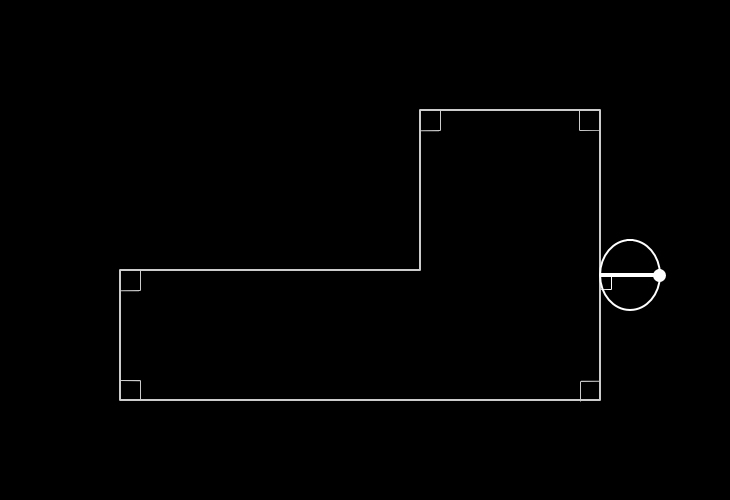
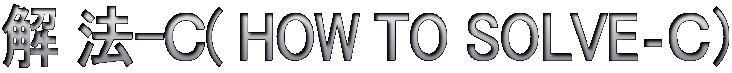⇒軌跡部分の面積の大きさが問われている場合、
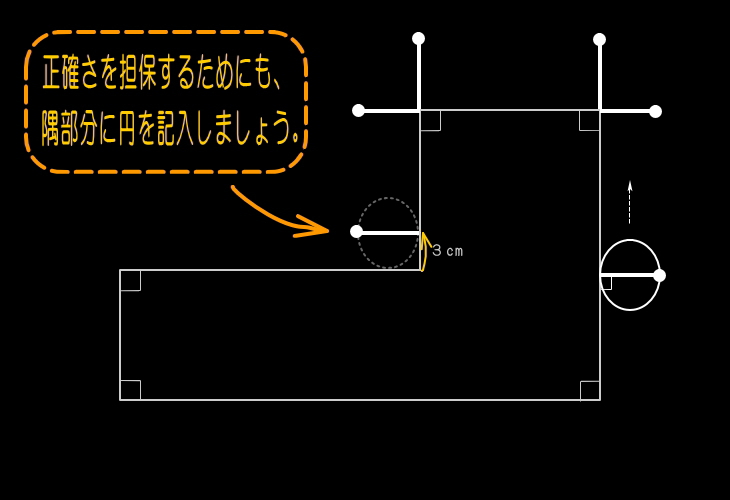
隅部分に注意する。
「軌跡部分には、含まれない。」
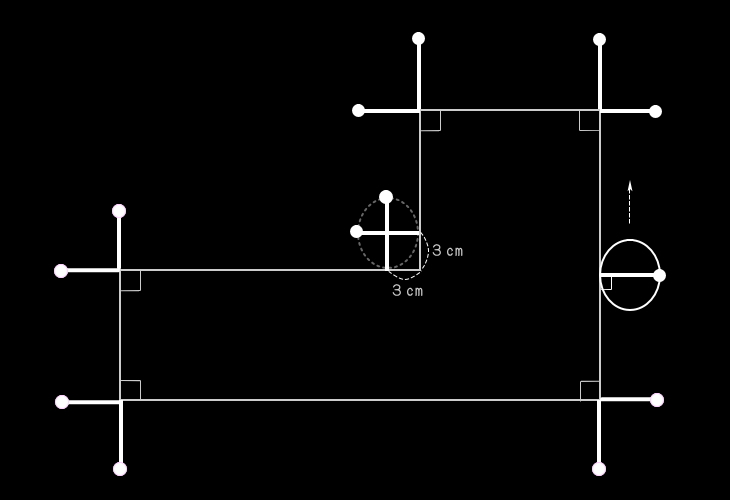
●目玉棒を、各辺と垂直をなす状態で移動させる。
その際、各辺の端にきたとき、その位置に目玉棒
を書き記す。
特に、基本となる作図法等には従わず、
例題などの解説に示されていた作図を思い出し、
与図へ大まかな作図を行う。
その後、立式を行い、進める。
●円の接点から、その接する辺と垂直をなし、かつ、
その長さが円の直径に相当する`目玉棒´を
その円の直径部分に書き記す。
この場合、次の目玉棒は、次の辺の端から
3cm内側の位置から移動させる。
その際、その位置に書き記すことを忘れずに。
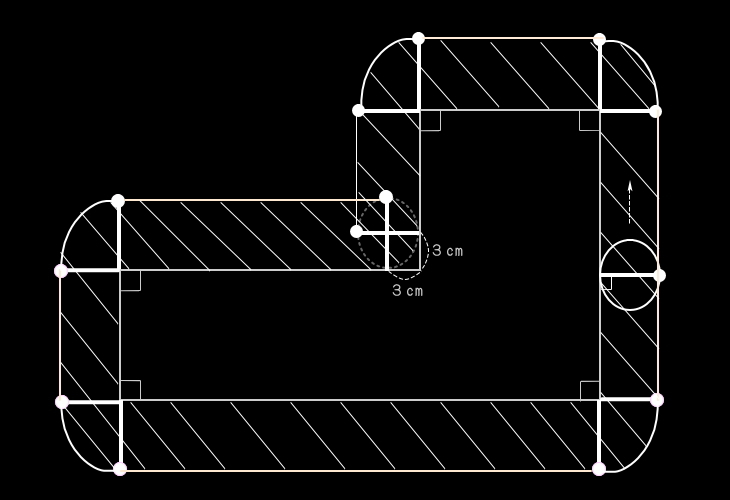
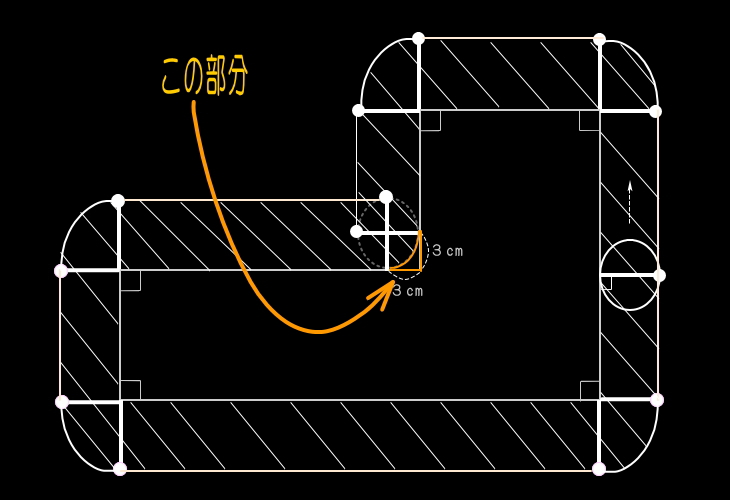
●問題文を読み返し、問われている部分を"太線"
や"斜線"などで加工する。
たとえば、この例で軌跡部分の面積であれば、…。
| EXAMPLE |
| 下図の外側を、直径3cmの円がこれを構成する各辺の上をすべることなく回転しながら移動します。 … 。 |
次のような手順に従い、基本となる作図法を用い、
解き進める。
たとえば、…。
●目玉棒が図形の各頂点を支点として回転する状態
をイメージしながら、必要な長さの"弧"で目玉
同士を結ぶ。
ただし、目玉棒を記入する際、
他の辺と重なる場合には、辺の端から
"半径の長さ分"内側に記入する。
●作図した与図を見ながら、立式・計算処理等を
行い、答えを求める。
●最後に、見直し…。
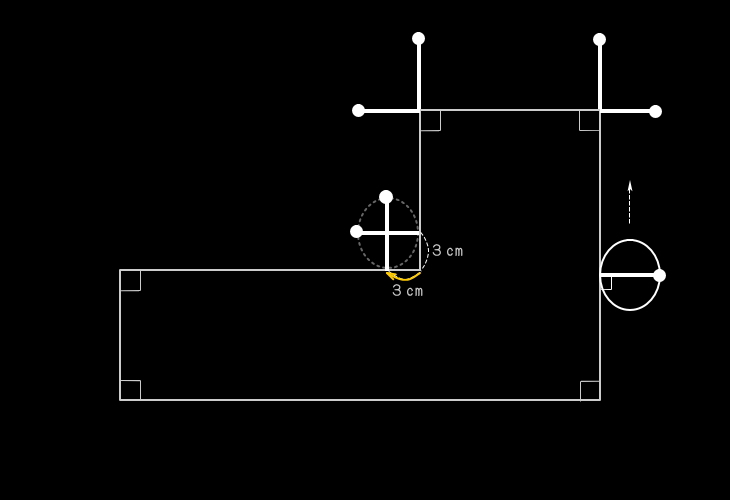
●各辺上に記入した目玉棒の"目玉"について、
同一辺上の目玉同士を"直線"で結ぶ。
与図への作図を殆ど行わず、
頭の中で、円の軌跡をイメージしながら、
式だけを用いて、進める。