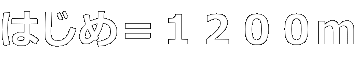今、若人達の意識の中核をなす内容は、
「 1分毎に、150mずつ、縮む。 」
とすれば、この意識に直結する質問…
つまり、
上の2つの図を見ている若人に対する質問内容は、
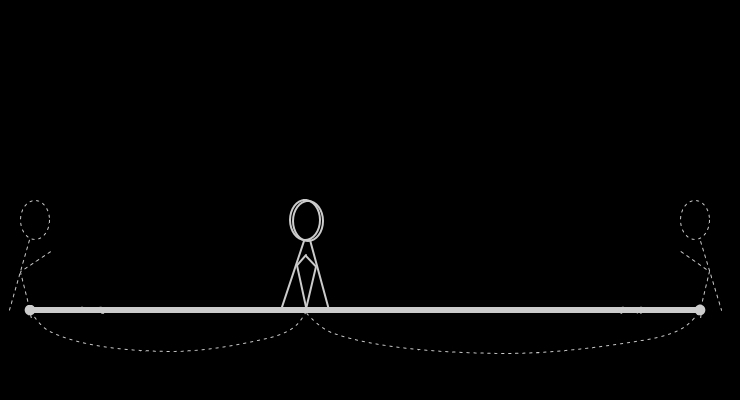
「2人が出会うまでに、
2人の間の道のりは、どれだけ縮んだ?」
⇒ ここでは、「2人が出会うまでに」という現象を
別の視点からみた際、「◎◎m縮むまでに」と
捉えることができるということが求められます。
最後に、
□ 「2人が出会うまでにかかる時間」
=「2人の間の道のりの長さが1200m縮む
までの時間」
□ 1分毎に150m縮む
ことを再確認し、立式等を通じて答えを求める。
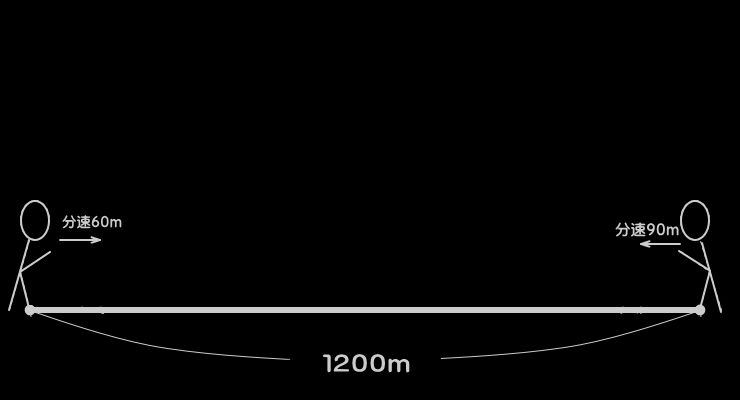
たとえば、
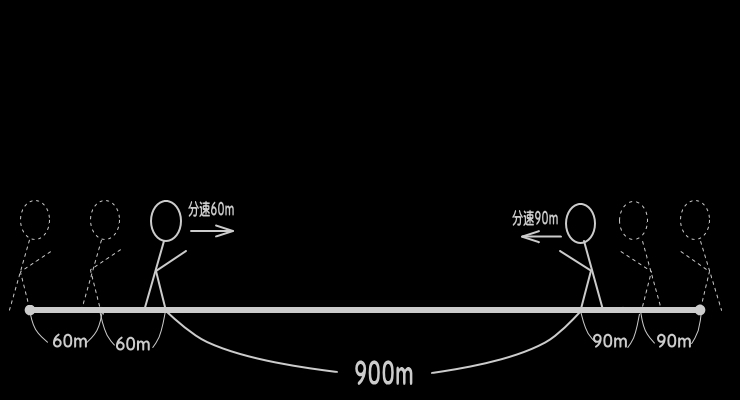
分速60mと分速90mの2人、
2人の間の道のりが1200m…
●同時に出発してから、
「単位時間(1分等)経つとどうなるのか」
を考える。
次のような順で考えながら、解き進める。
●向かい合って進む2人とその間の道のりを下図のよう
に記す。
⇒更に、単位時間経つと、
向かい合って進む2人の間の道のりは、同じく、
150m(2人の速さの和に相当する長さ分)縮む。
丸暗記した下記の式を用いる。
出会う迄にかかる時間
=(2人の間の道のり)÷(2人の速さの和)
「2人の間の道のりの長さ」について、
下記の特定の2つの時点に着眼する。
ここまで作成した図等から読み取れることは、
「 1分毎に、
2人の間の道のりは、
150mずつ、縮む。 」
である。
ここまでを、まとめると…
⇒単位時間経つと、向かい合って進む2人の間の道のり
は、150m(2人の速さの和に相当する長さ分)縮む。
●続いて、更に、
「単位時間(1分等)経つとどうなるのか」
を考える。